Una breve historia de las funciones En las matemáticas actuales el concepto de función se define del modo siguiente: Sean A y B conjuntos. Se llama función entre A y B a cualquier relación establecida entre los elementos de A y B de tal modo que a cada elemento de A le corresponde un único elemento de B. 1 Para representar las funciones se suele utilizar la notación: f : A → B para los conjuntos, f(x) = y para los elementos A se llama conjunto inicial y B es el conjunto final f(x) = y se expresa como y es la imagen de x a través de la aplicación f. Se pueden definir funciones entre cualquier tipo de conjuntos, pero las más interesantes son las que se establecen entre conjuntos de números. En los próximos temas vamos a estudiar funciones definidas en el conjunto de los números reales: las funciones reales (conjunto final) de variable real (conjunto inicial), f : R → R . La pregunta que cabe hacerse ahora es: ¿cómo se ha llegado hasta aquí?. Es importante entender que el concepto se desarrolló con el paso del tiempo; su significado fue cambiando y también la forma en que se definía, ganando precisión a través de los años. Lo más apropiado, quizás, sea comenzar en Mesopotamia2 . En las matemáticas babilónicas encontramos tablas con los cuadrados, los cubos y los inversos de los números naturales. Estas tablas sin duda definen funciones de N en N o de N en R, lo que no implica que los babilonios conocieran el concepto de función. Conocían y manejaban funciones específicas, pero no el concepto abstracto y moderno de función3 . En el antiguo Egipto también aparecen ejemplos de usos de funciones particulares. Una tabla con la descomposición de 2/n en fracciones unitarias4 para los impares n desde 5 hasta 101 aparece en el Papiro Rhind o Papiro Ahmes, de unos 4000 años de antigüedad considerado como el primer tratado de matemáticas que se conserva.
PAR ORDENADO
Un par de ordenado es un conjunto de dos elementos Ay B que tiene orden el elemento a la se la llama primera componente ya al elemento 2 componente se la representa simbólicamente con (a , b) no es lo mismo (a,b) que (b,a) ter ordenado
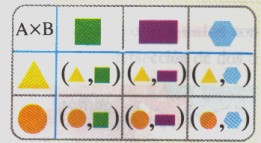
Producto cartesiano
Sea dos conjuntos A y B no vacíos denominaremos producto cartesianos entre A y B al conjunto de todo los pares ordenados cuya componente pertenece conjunto A y el segundo al conjunto B simbólicamente se la representa A*B
A*B={(X,Y)/(XEA)^(YEB)}
RELACIONES
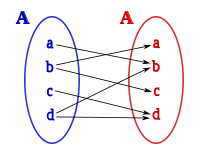
Una relación establece la correspondencia entre los elementos de dos conjuntos no vacio A y B .
Generalmente al conjunto de A se lo llama conjunto de partida, y el conjunto B, de llegada simbólicamente se lo representa así RÇ A*B
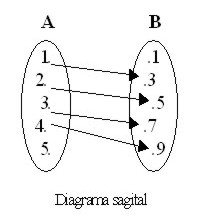
DOMINIO DE UNA RELACIÓN
Dando una relación construida partida un conjunto A Y B, los elementos del conjuntos A que establece correspondencia constituye el dominio de relación se representa don R
RANGO DE UNA RELACIÓN
Dando una relación construida partida de los conjuntos A Y B los elemento del conjuntos B que se relaciona con los elementos del dominio de constituye una rango de una relación.


RELACIÓN DE UNA FUNCIÓN
Correspondencia de un conjunto con otro
- dom R=A
- dom R


TIPOS DE FUNCIONES
FUNCIONES INYECTIVAS
F es inyectiva si cada elemento del rango es imagen inclusiva de único elemento del ademas la N(A)<= N (B)

FUNCIÓN SOBREYECTIVA
F es sobreyectiva si solo si rango es = B ademas N(A)>= N(B)
Biyectiva
Una función f (del conjunto A al B) es biyectiva si, para cada y en B, hay exactamente un x en A que cumple que f(x) = y
Alternativamente, f es biyectiva si es a la vez inyectiva y sobreyectiva.
Ejemplo: La función f(x) = x2 del conjunto de números reales positivos al mismo conjunto es inyectiva y sobreyectiva. Por lo tanto es biyectiva.
(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo
- f(2)=4 y
- f(-2)=4)

función real
Se llama función real de variable real a toda función definida de un subconjunto D de los números reales, en el conjunto R de los números reales, tal que a cada elemento x de D le corresponde uno y sólo un elemento y de R:
dominio e la función
sea F una función variable real f:x→ y. el conjunto x par el cual se encuentra definida conjunto F constituye el dominio de la función asimilación
simulación dom f
Rango de la función
se una función de variable real f: x→y , el conejuno de todo las imagen de los elemento dominio , constituye el rango de la función
f
se representa simbólicamente rgf
- Despejar x
- el rango sera el conjunto valores que tome la variable y
si f es una funcion de A en B entonces la gráfica de f es el conjunto pare o pares ordenadas de A EN B tales que sus coordenada son (x,y)
Criterio vertica vertical
si cualquier recta vertical intercesta la grafica en un solo punto e función
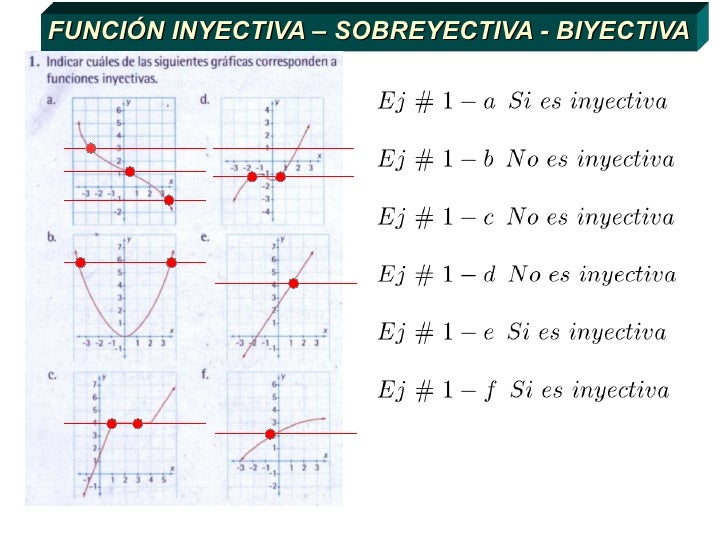
inyectiva

sobreyectiva
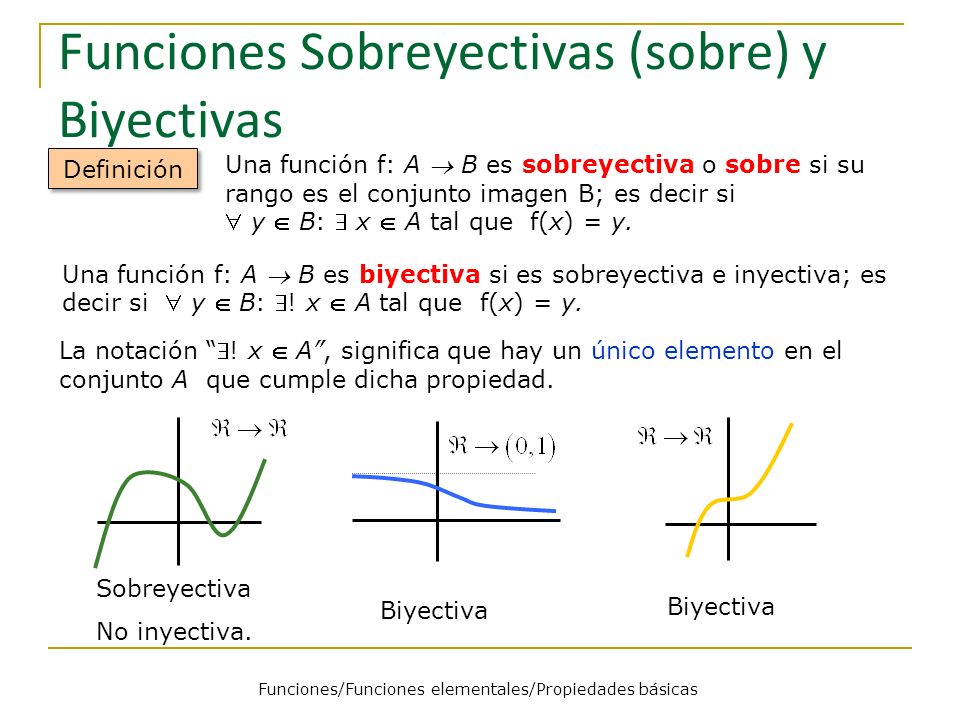
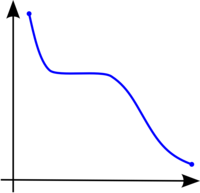
función decreciente
f es estrictamente decreciente en a si sólo si existe un entorno de a, tal que para toda x que pertenezca la entorno de a se cumple:



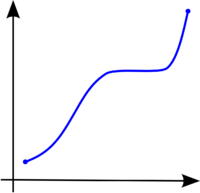
función creciente
es estrictamente creciente en a si sólo si existe un entorno de a, tal que para toda x que pertenezca la entorno de a se cumple:


función monotama
La función f es monótona si y sólo si x ≤ y implica f(x) ≤ f(y) (es decir, la función es creciente), o bien x ≤ y implica f(x) ≥ f(y) (es decir, la función es decreciente). En otras palabras, una función es monótona si conserva el orden.

función pares impares
e dice que una función es par si f(x) = f(-x), en el caso de que f(x) = -f(-x) se dice que la función es impar
Ejemplos 1:La función y(x)=x es impar ya que:
f(-x) = -x
pero como f(x) = x entonces:
f(-x) = - f(x).

Ejemplo 2:
Otra función impar es y = 1/x
Cuando f(x) = -f(-x)

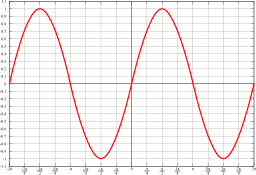
función periódica
En matemática, una función es periódica si los valores de la función se repiten conforme se añade a la variable independiente un determinado período, es decir:

- acotada
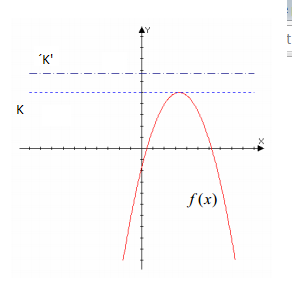
- Decimos que una función está acotada superiormente si existe un valor K tal que no es superado por ningún valor de la función, es decir: f(x)≤K para todo valor de x perteneciente al dominio, como podemos ver en la siguiente imagen:
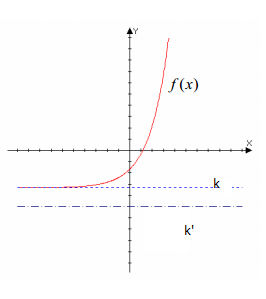
- acotada inferiormente
función por tramos
Las funciones definidas a trozos se llaman de esta manera porque tienen una definición diferente en cada tramo en el que están definidas. Por ejemplo,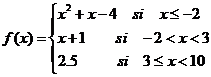
es una función definida a trozos, en cada “trozo” de su dominio tiene una definición.
Para valores de la variable menores o iguales que −2 la función está definida como x2 + x − 4 ; si la variable está entre −2 y 3 la función es x + 1 y entre 3 y 10 es igual a 2.5.
Observa, además, que su dominio de definición es (-∞, 10), porque no está definida para valores mayores o iguales que 10.
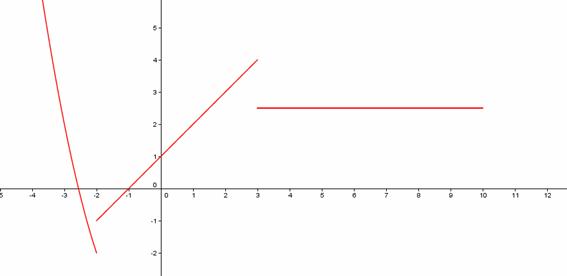
Su gráfica se compone de varios tramos o trozos.
función lineales
Sea A y B numero reales la función f: R —> R / f(x) = a.x+b donde a y b son números reales, es una función lineal.

ejemplos:
f (x) = 5x + 13
m = la pendiente es 5
b = 13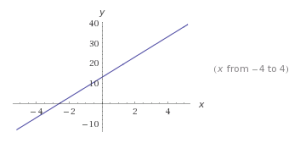


para los cortes Y se utiliza  ejemplos
ejemplos
 ejemplos
ejemplos
(A>o)^(b>0)

b) ; (a>o)^(b>0)
C):(a<0)^(b>0)
ejemplos
