Reseña historia
El origen de las matrices es muy antiguo. Los cuadrados latinos y los cuadrados mágicos se estudiaron desde hace mucho tiempo. Un cuadrado mágico, 3 por 3, se registra en la literatura china hacia el 650 a. C.2
Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un importante texto matemático chino que proviene del año 300 a. C. a 200 a. C., Nueve capítulos sobre el Arte de las matemáticas (Jiu Zhang Suan Shu), es el primer ejemplo conocido de uso del método de matrices para resolver un sistema de ecuaciones simultáneas.3 En el capítulo séptimo, "Ni mucho ni poco", el concepto de determinante apareció por primera vez, dos mil años antes de su publicación por el matemático japonés Seki Kōwa en 1683 y el matemático alemán Gottfried Leibniz en 1693.
Los "cuadrados mágicos" eran conocidos por los matemáticos árabes, posiblemente desde comienzos del siglo VII, quienes a su vez pudieron tomarlos de los matemáticos y astrónomos de la India, junto con otros aspectos de las matemáticas combinatorias. Todo esto sugiere que la idea provino de China. Los primeros "cuadrados mágicos" de orden 5 y 6 aparecieron en Bagdad en el 983, en la Enciclopedia de la Hermandad de Pureza (Rasa'il Ihkwan al-Safa).2
Después del desarrollo de la teoría de determinantes por Seki Kowa y Leibniz para facilitar la resolución de ecuaciones lineales, a finales del siglo XVII, Cramer presentó en1750 la ahora denominada regla de Cramer. Carl Friedrich Gauss y Wilhelm Jordan desarrollaron la eliminación de Gauss-Jordan en el siglo XIX.
En 1853, Hamilton hizo algunos aportes a la teoría de matrices. Cayley introdujo en 1858 la notación matricial, como forma abreviada de escribir un sistema de m ecuaciones lineales con n incógnitas.
Cayley, Hamilton, Hermann Grassmann, Frobenius, Olga Taussky-Todd y John von Neumann cuentan entre los matemáticos famosos que trabajaron sobre la teoría de las matrices. En 1925, Werner Heisenberg redescubre el cálculo matricial fundando una primera formulación de lo que iba a pasar a ser la mecánica cuántica. Se le considera a este respecto como uno de los padres de la mecánica cuántica.
Olga Taussky-Todd (1906-1995), durante la II Guerra Mundial, usó la teoría de matrices para investigar el fenómeno de aeroelasticidad llamado fluttering.
Matriz fila
Una matriz fila está constituida por una sola fila.

Matriz columna
La matriz columna tiene una sola columna

Matriz rectangular
La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn.

Matriz cuadrada
La matriz cuadrada tiene el mismo número de filas que de columnas.
Los elementos de la forma aii constituyen la diagonal principal.
La diagonal secundaria la forman los elementos con i+j = n+1, siendo n el orden de la matriz.

concepto asociado a matriz;
- Diagonal principal:
La que constituye los elementos de aij i=j

La traza
Es la suma de los elemento diagonal principal y se de nota (A)=15

Diagonal secundaria
La constituye y los elemento A y J que cumple la condición i+j=n+1

Matriz triangular superior.
es una matriz cuadrada que tiene todos los elementos bajo la diagonal principal igual a 0 esto es aij=0 si es mayor que j

Matriz triangular inferior
es una matriz cuadrada que tiene todos los elemento a sobre la diagonal principal igual a a 0.
esto es a y j o si y 0

Matriz nula
Que todo los elementos son iguales 0 y se lo representa o mxn

Matriz diagonal
Es una matriz cuadrada que tiene todo su elemento sobre y bajo diagonal principal=0 aij= o si ^#j

Matriz escalar
es una matriz cuadrada que tiene todo sus elemento sobre y bajo la diagonal principal iguales a o y los elemento diagonal principal son iguales entre si

Matriz identidad
Es una matriz cuadrada que tiene su elemento iguales a 0 excepto diagonl principal que son iguales a uno que se nota Imxn
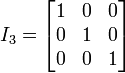
ENVESTIGACION
OPERACIONES ENTRE MATRICES
- SUMA Y RESTA ENTRE MATRICES: Dadas dos matrices de la misma dimensión, A=(aij) y B=(bij), se define la matriz suma como: A+B=(aij+bij).
La matriz suma se obtiene sumando los elementos de las dos matrices que ocupan la misma misma posición.
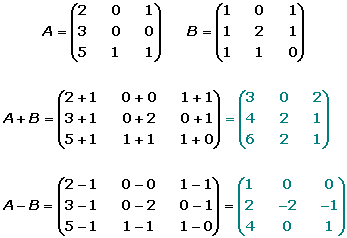
sumar o restar más de dos matrices se procede igual. No necesariamente para poder sumar o restar matrices, éstas tienen que ser cuadradas.
Ejemplo:
Sean
A =
|
-1
|
2
|
4
|
, B =
|
3
|
2
|
0
|
.
|
y C =
|
5
|
-1
|
3
| |||||
2
|
7
|
6
|
0
|
-3
|
-1
|
1
|
1
|
2
|
A + B + C =
|
-1
|
2
|
4
|
+
|
3
|
2
|
0
|
.
|
+
|
5
|
-1
|
3
|
=
|
7
|
3
|
7
| |||||||
2
|
7
|
6
|
0
|
-3
|
-1
|
1
|
1
|
2
|
3
|
5
|
7
|
A - B + C =
|
-1
|
2
|
4
|
-
|
3
|
2
|
0
|
.
|
+
|
5
|
-1
|
3
|
=
|
1
|
-1
|
7
| |||||||
2
|
7
|
6
|
0
|
-3
|
-1
|
1
|
1
|
2
|
3
|
11
|
9
|
Propiedades de la suma de matrices
Interna:
La suma de dos matrices de orden m x n es otra matriz dimensión m x n.
Asociativa:
A + (B + C) = (A + B) + C
Elemento neutro:
A + 0 = A
Donde O es la matriz nula de la misma dimensión que la matriz A.
Elemento opuesto:
A + (−A) = O
La matriz opuesta es aquella en que todos los elementos están cambiados de signo.
Conmutativa:A + B = B + A
MULTIPLICACIÓN DE MATRIZ POR ESCALAR
Dada una matriz A=(aij) y un número real k  R, se define la multiplicación de un número real por una matriz a la matriz del mismo orden que A, en la que cada elemento está multiplicado por k.
R, se define la multiplicación de un número real por una matriz a la matriz del mismo orden que A, en la que cada elemento está multiplicado por k.
 R, se define la multiplicación de un número real por una matriz a la matriz del mismo orden que A, en la que cada elemento está multiplicado por k.
R, se define la multiplicación de un número real por una matriz a la matriz del mismo orden que A, en la que cada elemento está multiplicado por k.
k · A=(k aij)
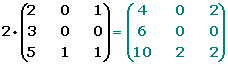
Propiedades
a · (b · A) = (a · b) · A A  Mmxn, a, b
Mmxn, a, b 

 Mmxn, a, b
Mmxn, a, b 

a · (A + B) = a · A + a · BA,B  Mmxn , a
Mmxn , a 

 Mmxn , a
Mmxn , a 

(a + b) · A = a · A + b · A A  Mmxn , a, b
Mmxn , a, b 

 Mmxn , a, b
Mmxn , a, b 

1 · A = A A  Mmx
Mmx
 Mmx
Mmx
multiplicación entre matriz
Dos matrices A y B son multiplicables si el número de columnas de A coincide con el número de filas de B.
Mm x n x Mn x p = M m x p
El elemento cij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos.

División de matrices
La división de matrices se define como el producto del numerador multiplicado por la matriz inversa del denominador. Es decir, sean las matrices A y B tal que A/B = AB-1:
Si una matriz está dividida entre un escalar, todos los términos de la matriz quedarán divididos por ese escalar.
Ejemplo:
Sean la matriz A =
|
8
|
16
|
, y k = 2 un escalar. En este caso:
| ||
3
|
-6
|

Determinante
DETERMINANTES DE UNA MATRIZ
A cada matriz cuadrada A se le asocia un número denominado determinante de A.
El determinante de A se denota por |A| o por det (A).
A = 

Determinante de orden uno
|a 11| = a 11
|5| = 5
Determinante de orden dos
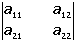 = a 11 a 22 - a 12 a 21
= a 11 a 22 - a 12 a 21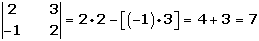
Determinante de orden tres
Consideremos una matriz 3 x 3 arbitraria A = (aij). El determinante de A se define como sigue:
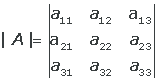 =
=
= a11 a22 a33 + a12 a23 a 31 + a13 a21 a32 -
- a 13 a22 a31 - a12 a21 a 33 - a11 a23 a32.
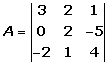 =
=
3 · 2 · 4 + 2 · (-5) · (-2) + 1 · 0 · 1 -
- 1 · 2 · (-2) - 2 · 0 · 4 - 3 · (-5) · 1 =
= 24 + 20 + 0 - (-4) - 0 - (-15) =
= 44 + 4 + 15 = 63
Obsérvese que hay seis productos, cada uno de ellos formado por tres elementos de la matriz.Tres de los productos aparecen con signo positivo (conservan su signo) y tres con signo negativo(cambian su signo).
Regla de Sarrus
La regla de Sarrus es una utilidad para calcular determinantes de orden 3.
Los términos con signo + están formados por los elementos de la diagonal principal y los de lasdiagonales paralelas con su correspondiente vértice opuesto.

Los términos con signo - están formados por los elementos de la diagonal secundaria y los de lasdiagonales paralelas con su correspondiente vértice opuesto.

Ejemplo

Menor complementario de un elemento de un determinante
Se llama menor complementario de un elemento aij al valor del determinante de orden n-1 que se obtiene al suprimir en la matriz la fila i y la columna j.

Adjunto de un elemento de un determinante
Se llama adjunto del elemento aij al menor complementario anteponiendo:
El signo es + si i+j es par.
El signo es - si i+j es impar.
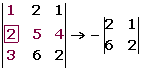
El valor de un determinante es igual a la suma de productos de los elementos de una línea por sus adjuntos correspondientes:





= 3(8+5) - 2(0-10) + 1(0+4) = 39 + 20 + 4 = 63
Cálculo de un determinante de cualquier orden
Consiste en conseguir que una de las líneas del determinante esté formada por elementos nulos, menos uno: el elemento base o pivote, que valdrá 1 ó -1 .
Seguiremos los siguientes pasos:
1.Si algún elemento del determinante vale la unidad, se elige una de las dos líneas: la fila o la columna, que contienen a dicho elemento (se debe escoger aquella que contenga el mayor número posible de elementos nulos).

2.En caso negativo:
1. Nos fijamos en una línea que contenga el mayor número posible de elementos nulos y operaremos para que uno de los elementos de esa línea sea un 1 ó -1 (operando con alguna línea paralela ).

2.Dividiendo la línea por uno de sus elementos, por lo cual deberíamos multiplicar el determinante por dicho elemento para que su valor no varie. Es decir sacamos factor común en una línea de uno de sus elementos.

3.Tomando como referencia el elemento base, operaremos de modo que todos los elementos de la fila o columna, donde se encuentre, sean ceros.
 4.Tomamos el adjunto del elemento base, con lo que obtenemos un determinante de orden inferior en una unidad al original.
4.Tomamos el adjunto del elemento base, con lo que obtenemos un determinante de orden inferior en una unidad al original. = 2(-58)
= 2(-58)Propiedades de los determinantes
1.|At|= |A|
El determinante de una matriz A y el de su traspuesta At son iguales.


2. |A|=0 Si:
Posee dos líneas iguales

Todos los elementos de una línea son nulos.

Los elementos de una línea son combinación lineal de las otras.

F3 = F1 + F2
3. Un determinante triangular es igual al producto de los elementos de la diagonal principal..

4. Si en un determinante se cambian entre sí dos líneas paralelas su determinante cambia de signo.

5. Si a los elementos de una línea se le suman los elementos de otra paralela multiplicados previamente por un nº real el valor del determinante no varía.


6. Si se multiplica un determinante por un número real, queda multiplicado por dicho número cualquier línea, pero sólo una.

7. Si todos los elementos de una fila o columna están formados por dos sumandos, dicho determinante se descompone en la suma de dos determinantes.

8. |A·B| =|A|·|B|
El determinante de un producto es igual al producto de los determinantes.