matemática para sistema: Trigometria

RESEÑA HISTÓRICA DE LA TRIGONOMÉTRICA

El estudio de la Trigometría lo inició Hiparco 150 años a. C. pero su historia se remonta a los egipcios y babilonios, primeros en medir ángulos.

Hiparco es considerado el padre de la Trigometría por sus contribuciones tales como determinar la duración del año solar en 365 días y 6 horas, sentar las bases de la trigometría, realizar el primer catálogo de estrellas (800) e inventar el primer astrolabio.

Tolomeo prosiguió los estudios de Hiparco. Ordenó los conocimientos de los griegos sobre astronomía, afirma que la tierra es redonda, y entre otras cosas realizó cálculos astronómicos sin utilizar las funciones trigonométricas.

A principios del siglo XVII, el matemático John Napier inventó los logaritmos y gracias a esto los cálculos trigonométricos recibieron un gran empuje. A med

iados de éste siglo Newton, utilizando series infinitas, encontró la serie para el sen x y series similares para el cos x y la tg x.

Por último, en el siglo XVIII, el matemático Leonhard Euler encontró la relación entre las propiedades trigonométricas y los números complejos.

ANGULOS Y SU MEDIDAS

Sistemas de medición de ángulos

ÁNGULOS DEFINICIÓN:

Dadas las semirrectas li y lt con origen común O, llamaremos ángulo a la porción de plano generada por el barrido de la semirrecta li hasta coincidir con lt. Se designa: li: lado inicial de a lt: lado terminal de a O: vértice del ángulo a Diremos que un ángulo se encuentra en posición normal si su vértice se ubica en el origen de coordenadas y su lado inicial coincide con el semieje positivo de las abscisas. a Si la rotación del lado terminal es en sentido contrario al de las agujas del reloj, la medida del ángulo será positiva, en caso contrario la medida será negativa. Generalmente se usan dos sistemas de medición: El sistema sexagesimal, cuya unidad es el grado: º Y el sistema radial cuya unidad es el radián: rad

Sistemas de Medición de Angulos

En la medida de ángulos, y por tanto en trigonometría, se emplean cuatro unidades, si bien la más utilizada en la vida cotidiana es el Grado sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la unidad natural para medir ángulos, el Grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción.

Radián: unidad angular natural en trigonometría, será la que aquí utilicemos. En una circunferencia completa hay 2π radianes.
Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.1º = 1R => 1R = 90º
90
Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.1^G = 1R => 1R = 100^G
100
Horario: su unidad de medida es el ángulo de 1 hora, que equivale a la sexta parte del ángulo recto.
Sistema Circular: La unidad de medida en este sistema es el radián.

Se llama radian al ángulo que abarca un arco de circunferencia cuya longitud es igual al radio de la misma.

Relación entre los Sistemas de medición de ángulos:

180º -------- π rad. ----------- 200^G----------- 12 hs

Equivalencias entre los distintos sistemas

Sistema Sexagesimal	Sistema Centesimal	Sistema Circular
90º	100^G	Π/2
180º	200^G	Π
360º	400^G	2Π

Ejemplos: Pasaje del sistema sexagesimal al circular y viceversa:

Cuando se desea pasar de un sistema a otro, se plantea y resuelve como un problema de regla de tres simple. Así:

*¿Cuántos radianes son 30º?

360º _______2π  rad
30º _______ x rad => x = 30º . 2π rad = π/6 rad
360º

*¿Cuántos grados son π/4 radianes?
2π rad ______ 360º
π/4 rad ______ xº => x = (π/4 rad) . 360º  = 45º
2π rad
CONVERSIÓN DE SISTEMA DE MEDICIÓN ANGULAR

CÍRCULOS TRIGONOMÉTRICAS
También conocido como trigonométrico, es aquel círculo cuyo centro coincide con el origen de coordenadas del plano cartesiano y cuyo radio mide la unidad.

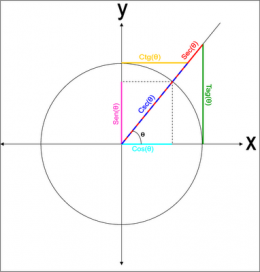
Características

Se toma como base un círculo de radio r = 1 con centro o, en el origen en el plano cartesiano. Se considera un ángulo arbitrario medido a partir del eje x positivo y en sentido positivo; o sea, en sentido contrario a las manecillas del reloj; todo ángulo puede ser colocado (y de una sola manera) de forma tal que su vértice coincida con el origen de coordenada , uno de sus lados (llamado lado inicial) coincide con la semirrecta OA y el otro lado (llamado lado terminal) quede ubicado ( a partir del inicial) en la zona de barrida en sentido contrario a la manecilla del reloj.

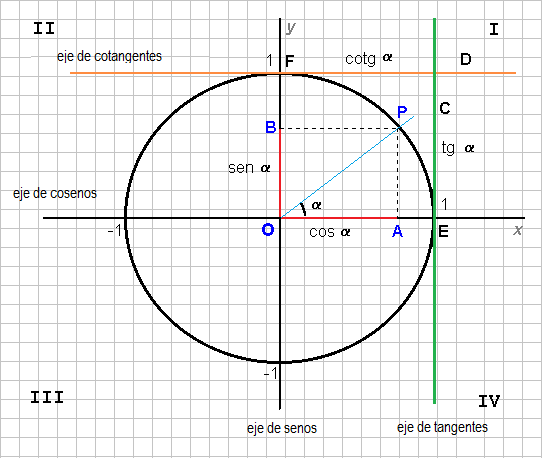
Razones trigonométricas

Si se rota la semirrecta OP de radio r rota hasta formar un ángulo α, si proyectamos el punto P hasta el eje X,Y, se obtienen dos segmentos; sobre el eje Y se proyecta el segmento OB denominado seno del ángulo α (Seno α), sobre el eje X se proyecta el segmento OA denominado coseno del ángulo α (cos α), formando un triángulo rectángulo OAP, cuyo lado AP se le denomina cateto opuesto al ángulo α, el lado OA es el cateto adyacente al ángulo α, mientras que el lado OP= r se denomina hipotenusa. Del triángulo rectángulo anterior podemos denotar las razones trigonométricas siguientes:

sen α = PA/r
cos α = OA/r
tang α = PA/OA
cot α= OA/PA

Seno del ángulo α

A partir del ángulo α y la semirrecta r se obtiene el punto P, al trazar una perpendicular desde dicho punto y hacia el eje Y se obtiene un segmento OB = AP que se denomina seno del ángulo α (se denota como sen α), también se determina a través de la razón (PA/r).

Coseno del ángulo α

A partir del ángulo α y la semirrecta r se obtiene el punto P, al trazar una perpendicular desde dicho punto y hasta el eje X se obtiene un segmento OA = BP que se denomina coseno del ángulo α (se denota como cos α), también se determina a través de la razón OA/r.

Tangente del ángulo α

Si trazamos una semirrecta EC tangente a la circunferencia por el punto E, que toque la semirrecta OD (prolongación de la semirrecta r), se forma el segmento EC que se denomina tangente del ángulo α (se denota como tang α); también se determina a través de la razón PA/OA.

Cotangente del ángulo α

Si trazamos una semirrecta FD, tangente al punto F y que toque la semirrecta OD, se forma un segmento FD denominado Cotangente del ángulo α (se denota como cot α); también se determina a través de la razón OA/PA.

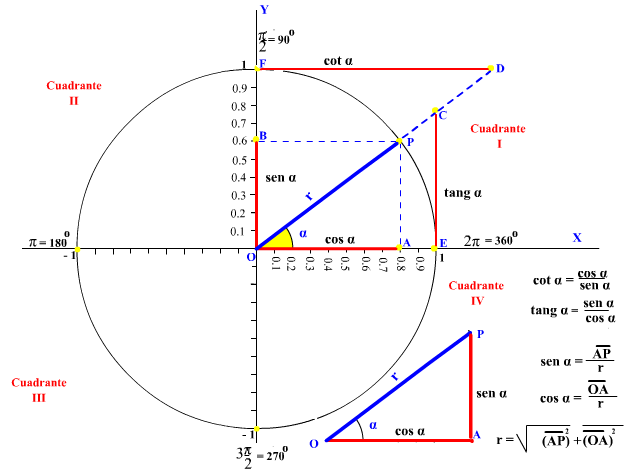
Cuadrantes del círculo trigonométrico

Si dividimos el círculo trigonométrico en 4 partes iguales se obtiene como resultado que cada [ángulo] consecutivo mide 90° (π/2 rd), cada una de las partes obtenidas se conoce como cuadrantes del círculo trigonométrico. En cada cuadrante los parámetros seno, coseno, tangente y cotange

e cambian su valor numérico con el aumento o disminución del ángulo α, este hecho lo corrobora las razones trigonométricas anteriores

Primer cuadrante

Parámetro Signo Seno + Coseno + Tangente + Cotangente +

En el primer cuadrante (I), con el aumento del [ángulo] α, disminuye el cos α y la cot α, mientras que aumenta la tang α y el sen α, hasta alcanzar su máximo o mínimo valor a 90° (π/2).

SEGUNDO CUADRANTE

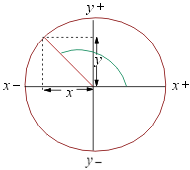En el segundo cuadrante (II), con el aumento del ángulo α, disminuyen el sen α y el cos α, por lo que lo hacen tambiéntang α y cot α, alcanzando su mínimo valor a 180° (π).

TERCER CUADRANTE

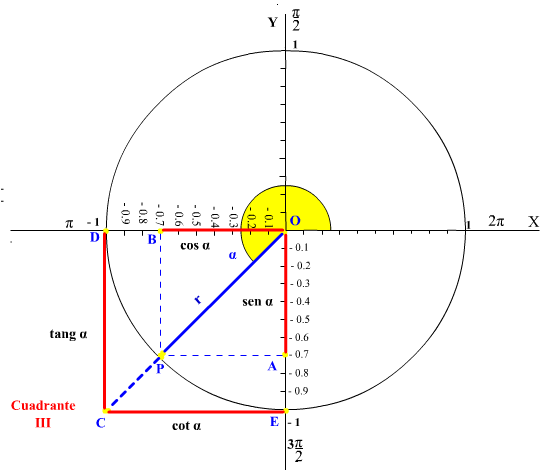
Parámetro Signo Seno - Coseno - Tangente + Cotangente +

En el tercer cuadrante (III), con el aumento del ángulo α, disminuyen el sen α y el cos α, la tang α aumenta su valor, mientras que la cot α disminuye dado que (a partir de que seno y el coseno son negativos y la relación existente entre ellos) hasta alcanzar su mínimo o máximo valor a 270° (3π/2).

CUARTO CUADRANTE

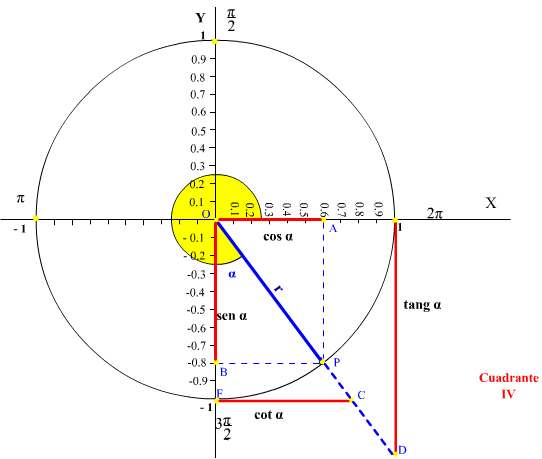
Parámetro Signo Seno - Coseno + Tangente - Cotangente -

En el cuarto cuadrante (IV), con el aumento del ángulo α, dirminuye el sen α, mientras que aumenta el cos α por lo que aumenta la cot α, mientras que disminuye la tang α y el, hasta alcanzar su máximo y mínimo valor a 360° (2π)

LINEAS TRIGONOMÉTRICA

Se llama circunferencia goniométrica a aquélla que tiene su centro en el origen de coordenadas y su radio es la unidad.

En la circunferencia goniométrica los ejes de coordenadas delimitan cuatro cuadrantes que se numeran en sentido contrario a las agujas del reloj.

QOP y TOS son triángulos semejantes.

QOP y T'OS′ son triángulos semejante

SIGNOS DE LAS RAZONES TRIGONOMÉTRICA

Resultado de imagen para SIGNOS DE RAZONES TRIGONOMETRICA

FUNCIONES TRIGONOMÉTRICA

GRÁFICA DE FUNCIONES TRIGONOMÉTRICA

CLASIFICACIÓN DE LAS FUNCIONES TRIGONOMÉTRICA

Resultado de imagen para clasificacion de las funciones trigonometricas

IDENTIDADES TRIGONOMÉTRICAS

Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas las funciones (y las operaciones aritméticas involucradas).