los números complejos, nos damos cuenta que es un sistema muy importante por integrar varias ramas de la matemática como lo son la trigonometría, la geometría y el álgebra, entonces resulta bastante interesante indagar un poco más acerca de este tema, comenzando por su historia.
Isaac Asimov, en su libro “De los números y su historia”, relata una historia en la que un profesor de Sociología en su clasificación de la humanidad agrupó a los matemáticos entre los místicos junto con los poetas y los teólogos, ya que para él los matemáticos son místicos porque creen en números que no tienen realidad, para explicarlo dijo lo siguiente, “La raíz cuadrada de menos uno. No tiene existencia. Los matemáticos lo llaman imaginario. Pero de alguna manera mística creen que tiene alguna clase de existencia”. Pero la verdad es que no hay nada de místico en ellos, son tan reales como cualquier otro.
Los números complejos aparecieron muy temprano en las matemáticas, pero fueron ignorados, por ser para la mayoría un poco extraños y difíciles de representar. Al comienzo los hombres solamente aceptaban los números naturales por ser los más adecuados para contar objetos que comúnmente se consideran como unidades. Pero al medir magnitudes como la longitud o el peso, las fracciones se hicieron imprescindibles. Los egipcios y babilonios se las arreglaron para elaborar métodos que les permitieron operar con fracciones. Pero los griegos descubrieron que habían cantidades definidas que no podían ser expresadas como cocientes de números enteros, la noción de número extiende más allá, ya que los griegos no aceptaban que hubieran números menores que el cero. Los números complejos aparecen entre las soluciones de las ecuaciones cuadráticas, que generan raíces cuadradas de números negativos los cuales no poseen soluciones reales. Los matemáticos griegos que conocían métodos geométricos de resolución, consideraban estos problemas irresolubles, rechazaban el uso de números negativos por la falta de un equivalente dentro de la geometría que para ese momento era el centro de la matemática. El surgimiento de los números complejos no se debió solo a la imposibilidad de resolver algunas ecuaciones cuadráticas, sino que viene también de las ecuaciones cúbicas. Más adelante con el surgimiento del álgebra durante la Edad Media, el concepto de número se amplía para manipular ecuaciones, desligadas de la geometría.
Los números complejos aparecieron muy temprano en las matemáticas, pero fueron ignorados, por ser para la mayoría un poco extraños y difíciles de representar. Al comienzo los hombres solamente aceptaban los números naturales por ser los más adecuados para contar objetos que comúnmente se consideran como unidades. Pero al medir magnitudes como la longitud o el peso, las fracciones se hicieron imprescindibles. Los egipcios y babilonios se las arreglaron para elaborar métodos que les permitieron operar con fracciones. Pero los griegos descubrieron que habían cantidades definidas que no podían ser expresadas como cocientes de números enteros, la noción de número extiende más allá, ya que los griegos no aceptaban que hubieran números menores que el cero. Los números complejos aparecen entre las soluciones de las ecuaciones cuadráticas, que generan raíces cuadradas de números negativos los cuales no poseen soluciones reales. Los matemáticos griegos que conocían métodos geométricos de resolución, consideraban estos problemas irresolubles, rechazaban el uso de números negativos por la falta de un equivalente dentro de la geometría que para ese momento era el centro de la matemática. El surgimiento de los números complejos no se debió solo a la imposibilidad de resolver algunas ecuaciones cuadráticas, sino que viene también de las ecuaciones cúbicas. Más adelante con el surgimiento del álgebra durante la Edad Media, el concepto de número se amplía para manipular ecuaciones, desligadas de la geometría.
Se considera al matemático árabe Al-Khwarizmi como el padre del Álgebra, fue el autor de un libro titulado al-jabr, publicado en el año 830 d.c. Este libro fue de gran influencia por recoger todas las técnicas conocidas hasta entonces sobre la resolución de ecuaciones de primero y segundo grado. Traducido al latín por Gerardo de Cremona, se utilizó en las universidades europeas hasta el siglo XVI. Es posible que antes de él se hubiesen resuelto ecuaciones concretas, pero éste es el primer tratado conocido en el que se hace un estudio exhaustivo. Los matemáticos árabes se encargaron de difundir las matemáticas de los griegos, mesopotamios e hindúes en toda Europa, a través de España.
El primer matemático que empleó sistemáticamente los números menores que el cero fue el Italiano Girolamo Cardano, quien decía que después de todo puede haber algo menos que nada, “una deuda es menos que nada”. Cardano fue un célebre matemático italiano delRenacimiento, físico, astrólogo y jugador de juegos de azar. Nació enPavía, Italia, hijo ilegítimo de un abogado con talento para las matemáticas quien fue amigo de Leonardo Da Vinci. Se gradúa de Médico en la Universidad de Papua. Después de recibir el título de Doctor en Medicina se dedica a ejercer su profesión, pero también al juego de cartas, dados y ajedrez. Su afición por el juego lo llevó a estudiar y desarrollar muchas técnicas de la teoría de las probabilidades y las aplicó de manera exitosa logrando hacer una fortuna como jugador. Hoy, es más conocido por sus trabajos de álgebra. En 1539 publicó su libro de aritmética “Practica arithmetica et mensurandi singulares”. Publicó las soluciones a las ecuaciones de tercer y cuarto grado en su libro “Ars magna” datado en 1545.
En cuanto a lo expuesto en el libro “Ars magna” por Cardano, hay una historia bastante interesante que merece ser tratada. En el año 1539, Cardano conoce al matemático de Niccolò Fontana (más conocido comoTartaglia), lo cual fue un hecho crucial en su vida, pues desde ese momento comienza a interesarse por las ecuaciones cúbicas. Tartaglia era un matemático de reconocido prestigio, entre otras cosas, por haber ganado concursos sobre la resolución de ecuaciones. Huérfano y sin medios materiales para proveerse una instrucción, llegó a ser uno de los principales matemáticos del siglo XVI. Explicó esta ciencia sucesivamente en Verona, Vicenza, Brescia y finalmente Venecia, ciudad en la que falleció en 1557.
Descubridor de un método para resolver ecuaciones de tercer grado, estando ya en Venecia, en 1535 su colega del Fiore discípulo de Scipione del Ferro de quien había recibido la fórmula para resolver las ecuaciones cúbicas, le propone un duelo matemático que Tartaglia acepta. A partir de este duelo y en su afán de ganarlo Tartaglia desarrolla la fórmula general para resolver las ecuaciones de tercer grado. Por lo que, consigue resolver todas las cuestiones que le plantea su contrincante, sin que éste logre resolver ninguna de las propuestas por Tartaglia.
Tartaglia le enseñó a Cardano sus trucos y técnicas secretas para el manejo de las ecuaciones, no sin antes hacerle prestar un juramento de no revelar a nadie dichos secretos. Sin embargo, en vista de que Tarataglia no publica su fórmula, y que según parece llega a manos de Cardano un escrito inédito de otro matemático fechado con anterioridad al de Tartaglia y en el que independiente se llega al mismo resultado, será finalmente Cardano quien, considerándose libre del juramento, en 1545, publica su obra “Ars Magna” donde expone los métodos para la resolución de la ecuación cúbica. Tartaglia acusa a Cardano de traidor y deshonesto, por haber faltado a su juramento. Salió en defensa de Cardano, un joven matemático que era su discípulo, Lodovico Ferrari.
Cardano hizo uso por vez primera de las raíces cuadradas de números negativos y consideró la posibilidad de usar los números imaginarios. Fueron entre las soluciones de la ecuación cúbica en el libro de Cardano donde se dió el nacimiento de los números complejos.
A raíz de la polémica entre Cardano y Tartaglia, Rafael Bombelli, algebrista italiano, nacido en 1526 en Bolonia, quien había leído el “Ars Magna” de Cardano a los 19 años, decidió escribir un tratado de álgebra que permitiese a cualquiera dominar el tema sin recurrir a ningún otro libro. Bombelli conocía bien los trabajos sobre ecuaciones cúbicas de Cardano y consideraba aquel libro como el más interesante de todos los escritos sobre álgebra, hasta el momento. Sin embargo pensó que algunas cosas estaban todavía algo confusas y que se podían hacer mucho más comprensibles para el público.
Bombelli puede ser llamado el padre de los números complejos, pues fue el primero que desarrolló el álgebra formal para trabajar con las expresiones de la forma . En la fórmula de Cardano, mejor conocida como la fórmula del Ferro-Tartaglia-Cardano aparecen dos sumandos del tipo , la idea de Bombelli es reducir dicho número a uno del tipo . En el libro “L’Algebra” aparecen por primera vez el cálculo con los números negativos, así como también las reglas para sumar y multiplicar dichos números. El gran aporte de Bombelli al álgebra, fue el de aceptar sin reserva la existencia de , como un número.
Euler intentó comprender qué eran realmente los números complejos y en su "Vollständige Auleitung zur Algebra" (Introducción Completa al Algebra), que apareció primero en Rusia en 1768-69 y en Alemania en 1770, y es el mejor texto de álgebra del siglo XVIII dice:
"Puesto que todos los números concebibles son mayores que cero, menores que cero, o iguales a cero, está claro que las raíces cuadradas de números negativos no pueden ser incluidas entre los números posibles (reales). En consecuencia debemos decir que son números imposibles. Y esta circunstancia nos lleva al concepto de tales números, que por su naturaleza son imposibles, y ordinariamente se les llama imaginarios o ideales, porque existen sólo en la imaginación".
En 1777 el matemático Leonhar Euler introdujo el símbolo (por imaginario), que después se adoptó de manera general. De modo que podemos escribir , o bien . Habiendo definido i de esta manera, podemos expresar la raíz cuadrada de cualquier número negativo. En general cualquier raíz cuadrada de un número negativo , se puede escribir como la raíz cuadrada del número positivo correspondiente por la raíz cuadrada de menos uno, es decir . Cualquier número que combine unidades reales e imaginarias se denomina “complejo”.
Los números reales son solamente casos especiales de los números complejos, como también lo son los números imaginarios. Si uno representa los números complejos de la forma , entonces los números reales son todos aquellos complejos en que es igual a cero. Y los números imaginarios son todos los complejos en los que es igual a cero.
Para finalizar debemos mencionar que en 1799 el matemático alemán Carl Gauss dio su primera demostración del teorema fundamental del álgebra, en el que establece que todo polinomio con coeficientes complejos se descompone en factores lineales, es decir, que tiene todas sus raíces en , y puesto que ésta dependía necesariamente del reconocimiento de los números complejos, Gauss consolidó la posición de estos números. En 1831 Gauss publica un trabajo donde expone con toda claridad las propiedades de los números de la forma , llamados ahora Números de Gauss, y la representación geométrica de los mismos. A partir de todas esas investigaciones se inicia un desarrollo sostenido de la teoría de las funciones complejas
Representación
definición de números complejo
Definiremos cada complejo z como un par ordenado de números reales (a, b) ó (Re(z), Im(z)), en el que se definen las siguientes operaciones:
- Suma
- Producto por escalar
- Multiplicación
- Igualdad
A partir de estas operaciones podemos deducir otras como las siguientes:
- Resta
- División
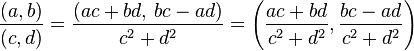
- unidad imaginaria
- La unidad imaginaria es el número
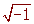 y se designa por la letra i.
y se designa por la letra i.

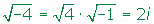
- potencias

- ejemplos

Un número complejo se constituye por una parte real y una imaginaria, representadas en forma rectangular por:

Ecuación 2.1
Donde i es la parte imaginaria y x es la parte real y y es un número real. Para no generar confusión con el manejo de la corriente eléctrica con la parte imaginaria (i), se trabaja de la siguiente forma:

conjugado de numero complejos
Se llama complejo conjugado de un numero ´ z = x + iy al numero ´ z = x − iy. Para z se cumple
que:


Operaciones
Igualdad
Dos números complejos son iguales cuando sus partes reales y sus partes imaginarias son iguales entre sí.
a + bi = c + di quiere decir a = c y b = d
Ejemplo:
Determina para qué valores de x e y son iguales los números complejos: z = x -3 + 5i,
w = 4 + (y + 4)i
Igualamos por separado las partes reales x -3 =4 y se obtiene x =7 y las partes imaginarias
5 = y + 4, se obtiene y = 1.
Luego para que sean iguales debe cumplirse que x = 7 e y = 1.
Operaciones con números complejos:
Para sumar (restar) dos números complejos se suman (restan) las partes reales entre sí, y luego las partes imaginarias
z + w = (a +bi) + (c + di) = (a +c) + (b + d)i
El resultado es un número complejo de parte real la suma (resta) de las partes reales y de parte imaginaria la suma(resta ) de las partes imaginarias.
En el siguiente enlace pudimos observar el significado gráfico de la suma y la resta. Esperamos que contestéis las preguntas que aparecen en la página en los comentarios.
Propiedades de los Conjugados
· Primera propiedad
El conjugado del conjugado de un complejo z es el propio z.
Demostración:
si z = a + bi se tiene que = a - bi , de donde, = a + bi = z
· Segunda propiedad
Dados dos números complejos cualesquiera z y z' , el conjugado de su suma es igual a la suma de sus conjugados.
Demostración:
Tomando : z = a + bi y z' = c + di
Se obtiene:
a + bi y ' = c - di
Con lo que:
(a + bi ) + (c - di ) = (a + c) + (-b - d)i
· Tercera propiedad
El conjugado del producto de dos números complejos es igual al producto de los conjugados de dichos números:
Demostración:
Si z = a + bi y z = c + di
Se tiene que z · z = (ac - bd ) + (ad + bc)i
Cuyo conjugado es (ac - bd) - (ad + bc)i .
Calculando por otro lado el producto de los conjugados, resulta que
(a - bi )( c - di ) = ( ac - bd ) + ( -ad - bc) i .
· Cuarta propiedad
Los complejos que coinciden con sus conjugados son los números reales.
Demostración:
Sea un complejo a + bi que coincida con su conjugado.
Esto equivale a que:
a + bi = a - bi
Pero esto sólo ocurre si b = 0, es decir si a + bi es un número real.
· Quinta propiedad
La suma y el producto de un complejo y su conjugado son, ambos, números reales.
Demostración: (a + bi ) + (a - bi ) = 2a
(a + bi ) (a - bi ) = a2 - (bi )2 = a2 + b2
Complejo opuesto
Dado un número complejo (x,y) el complejo opuesto sería (-x,-y)
Si al número complejo lo representamos por n, el complejo opuesto se representa por n'.
Si z = a +bi
El opuesto de z seria -z = -a - b
El Conjugado de z seria z = a + bi
Operaciones con Números Complejos
Suma de Números Complejos
Dados dos números complejos a + bi y c + di se definen su suma como:
(a + bi ) + (c + di ) = (a + c) + (b + d)i
Propiedades de la Suma de Números Complejos
La suma de números complejos tiene las siguientes propiedades:
· Conmutativa
Dados dos números complejos a + bi y c + di se tiene la igualdad:
(a + bi ) + (c + di ) = (c + di ) + (a + bi )
Ejemplo:
(2 - 3i ) + (-3 + i ) = (2 - 3) + i (-3 + 1) = -1 - 2i
(-3 + i ) + (2 - 3i ) = (-3 + 2) + i (1 - 3) = -1 - 2i
· Asociativa
Dados tres complejos a + bi, c + di y e + fi , se cumple:
[(a + bi ) + (c + di )] + (e + fi ) = (a + bi ) + [(c + di ) + (e + fi )]
Ejemplo:
[(5 + 2i ) + (3 - 4i )] + (-9 + 8i ) = (8 - 2i ) + (-9 + 8i ) = -1 + 6i
(5 + 2i ) + [(3 - 4i ) + (-9 + 8i )] = (5 + 2i ) + (-6 + 4i ) = -1 + 6i
· Elemento neutro
El elemento neutro es 0 + 0i , puesto que
(a + bi ) + (0 + 0i ) = (a + 0) + i (b + 0) = a + bi
El número 0 + 0i se escribe simplificadamente 0 y se le llama «cero».
· Elemento simétrico
El elemento simétrico de un número complejo cualquiera a + bi es (- a - bi ):
(a + bi ) + (-a - bi) = 0 + 0i = 0
Ejemplo:
El simétrico de 2 - 3i es -2 + 3i pues (2 - 3i ) + (-2 + 3i ) = 0
Producto de Números Complejos
La multiplicación se efectúa igual que si fuesen números reales, pero teniendo en cuenta que la multiplicación de complejos no es equivalente al producto escalar de vectores.
Dados dos números complejos a + bi y c + di se definen su producto como:
(a + bi ) (c + di ) = (ac - bd) + (ad + bc)i
El producto puede hacerse operando con i como si fuese un número real y teniendo en cuenta que i 2 = -1.
(a + bi )(c + di ) = ac + adi + bci + bdi 2 = ac + i(ad + bc) + bd(-1) = ac - bd + i (ad + bc)
Pero para comprobar resultados, podemos representar los complejos que se multiplican por sus vectores, y el resultado del producto por el vector correspondiente al complejo producto.
Propiedades del Producto de Complejos
· Conmutativa
Dados dos complejos a + bi y c + di , se cumple que:
(a + bi ) (c + di ) = (c + di ) (a + bi )
· Asociativa
Dados los complejos a + bi, c + di y e + fi se cumple que:
[(a + bi ) (c + di )](e + fi ) = (a + bi ) [(c + di ) (e + fi )]
· Elemento neutro
El elemento neutro del producto es 1 + 0 ·i = 1, puesto que para cualquier complejo a + bi , (a + bi ) (1 + 0 · i ) = (a + bi ) · 1 = a + bi . El elemento neutro es el uno.
· Distributiva del producto con respecto a la suma
Dados tres números complejos a + bi , c + di y e + fi , se cumple:
(a + bi ) [(c + di ) + (e + fi )] = (a + bi ) (c + di ) + (a + bi ) (e + fi )
Ejemplo:
(1 - 2i ) [3i + (2 - 7i )] = (1 - 2i ) (2 - 4i ) = 2 - 4i - 4i + 8i 2 = -6 - 8i
(1 - 2i ) 3i + (1 - 2i ) (2 - 7i ) = (3i - 6i 2) + (2 - 7i - 4i + 14i 2) = (3i + 6) + (-12 - 11i )
= - 6 - 8i
El conjunto de los números complejos, por contar con todas las propiedades anteriores para la suma y para el producto, se dice que es un anillo conmutativo.
El conjunto de los números complejos se simboliza por C, o también (C, +, ·).
EJEMPLOS

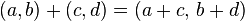


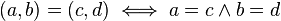

No hay comentarios:
Publicar un comentario